| V I S U A L I Z Z A D I S C U S S I O N E |
| baldiniantonio |
Inserito il - 22/06/2017 : 12:07:25
prova d'esame!
http://www.iltempo.it/cronache/2017/06/22/news/maturita-via-alla-seconda-prova-d-esame-1030546/
|
| 11 U L T I M E R I S P O S T E (in alto le più recenti) |
| Ibla |
Inserito il - 25/06/2017 : 16:58:41
 |
| @lby64 |
Inserito il - 25/06/2017 : 07:59:22
Cosa???
Ma neanche quando ero pronto x Analisi2 ce l'avrei fatta!
Esame di Maturita?
Ma non ci credo!!!
 |
| pixbuster |
Inserito il - 25/06/2017 : 00:23:16
meno male che il problema prevedeva una pedana rettilinea su cui far andare la ruota quadra perchè quella del Momath è circolare ed ha "infinite" curve man mano che ci si allontana dal centro della pedana
|
| baldiniantonio |
Inserito il - 24/06/2017 : 19:14:18
bravi tutti ma...
http://matematica.unibocconi.it/sites/default/files/Problema%201_2017.pdf |
| @lby64 |
Inserito il - 24/06/2017 : 14:57:26
Ok, causa paralisi in casa per eccesso di calore ci ho provato.
Come quando riprovai a giocare a tennis trovando che tra il ricordo di ciò che
sapevo fare e ciò che ero effettivamente in grado di fare c'era un oceano
così ho trovato il problema troppo complicato.
Ho calcolato la traiettoria del centro ma mi sono reso conto che non è ciò che serve.
Comunque attendo x vedere la soluzione, magari mi viene fuori tempo massimo.
Bocciato!
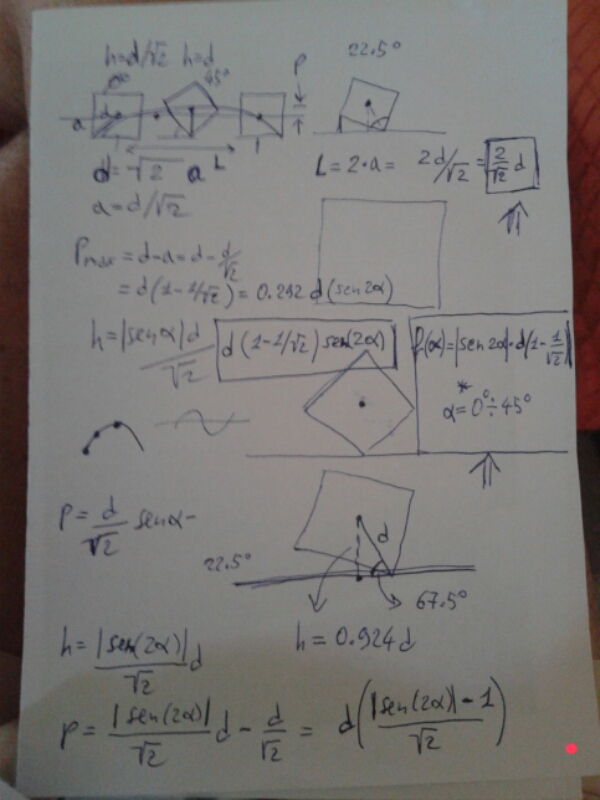
Allego solo x testimonianza dell'immane sforzo!
Immagine:
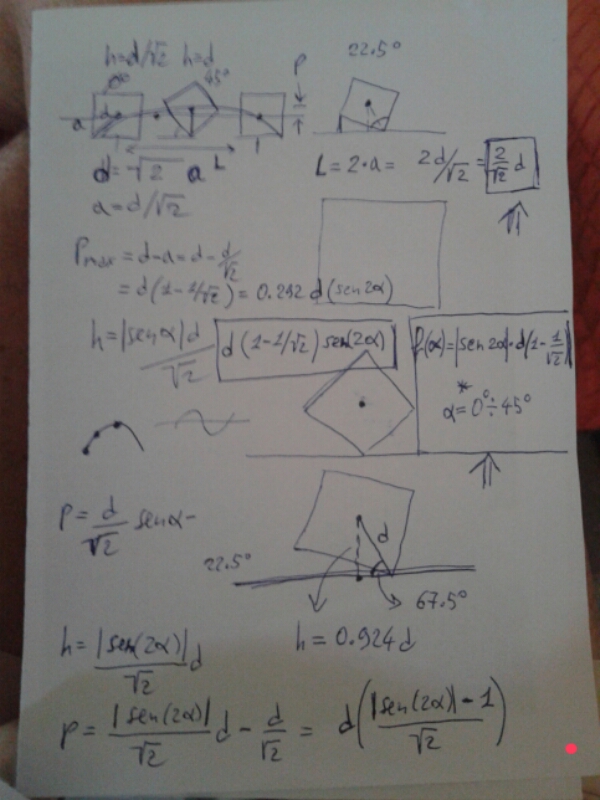
290,29 KB |
| @lby64 |
Inserito il - 24/06/2017 : 11:33:50
Lo spirito era proprio quello!
Ciao!
|
| giordano5847 |
Inserito il - 24/06/2017 : 10:19:39
sarà una semicirconferenza ed i punti da considerare sono a 0, 22,5, e 45° esattamente lo sviluppo di un lato del quadrato/ruota.
Giusto considerare il centro di rotazione della ruota che gira attorno al centro della traettoria per un angolo che comprende gli "end" della semi c. (in pratica ne delimita il dia quindi il raggio).
Stò ragionando a voce alta (ho 70anni ed ho fatto trigonometria ai periti ) |
| @lby64 |
Inserito il - 24/06/2017 : 09:24:48
Non dubito.
Comunque trattasi di curva di secondo grado quindi determinati tre punti (rotazione 0, 45, 90 gradi x esempio) dell'altezza del centro ruota dal suolo al ruotare della ruota con una equazione di secondo grado si dovrebbe determinare la curva da compensare con il profilo ondulato del terreno (una ruota è tale se il centro non varia, altrimenti è sbilenca).
Altre idee?
|
| SHILAH |
Inserito il - 24/06/2017 : 08:20:35
Lo svolgimento del tema era tutt'altro che banale. |
| @lby64 |
Inserito il - 23/06/2017 : 12:46:35
Visto che nelle nostre strade continuano a far passare tubi e cavi
trasformandole di fatto in ondulati si mettessero daccordo
almeno per distanziarle uniformemente che alla prossima ebike
le ruote quadrate ce le metto anch'io.
A proposito, senza fare i conti, l'ondulazione deve essere un'arco di parabola o di sinusoide?
A naso essendoci di mezzo angoli e rotazione propenderei per la second ma non faccio trigonometria da decenni!
|
| baldiniantonio |
Inserito il - 22/06/2017 : 16:25:47
esiste!
http://www.repubblica.it/speciali/scuola/maturita/edizione2017/2017/06/22/foto/momath_museum_new_york_seconda_prova_matematica-168787757/1/?ref=RHPPLF-BL-I0-C8-P3-S2.4-T1
|
]
